# 基于目标的矢量场寻路
Understanding Goal-Based Vector Field Pathfinding https://gamedevelopment.tutsplus.com/tutorials/understanding-goal-based-vector-field-pathfinding–gamedev-9007
本文讲解矢量场寻路,以及它相对于传统寻路算法的优势,传统算法比如Dijkstra’s算法。对 [Dijkstra’s algorithm](https://en.wikipedia.org/wiki/Dijkstra’s_algorithm ) 和 [potential fields](http://aigamedev.com/open/tutorials/potential-fields/) 的基础理解会更加利于理解本文。
## 简介
寻路有很多解决方案,每种方案各有利弊。许多寻路算法都是为每个寻路计算出一条到达目的地的路径,这意味着有越多的寻路就会有越多翻倍的计算量。这在很多情况下是可接受的,但在有成千上万的寻路需要时,需要有更高效的方式才行。
矢量场寻路,这种方式计算图中从目标到每个节点的路径。为了巩固说明,我会用我自己实现的专用例子来解释这个算法。
注意:矢量场寻路通常可被抽象为节点和图;尽管我采用的网格方式,但并不意味着这个算法只限于基于网格的世界。
## 视频概述
矢量场寻路分三步:
– 创建一个热力图,描述地图上每个节点到目标的路径距离
– 创建一个矢量场,指出走向目标的朝向。
– 所有寻找该公共目标的粒子都使用这矢量场来导航至目标。
视频显示了最终效果,并给你下文完整教程这个概念的全面概览。
## 生成热力图
热力图存储着这张地图上每个点到目标点的路径距离。路径距离和欧几里得距离不同之处在于,它是仅途经可通行地形上两点间的距离。比如GPS总是计算路径距离,对他来说,公路就是唯一可通行地形。
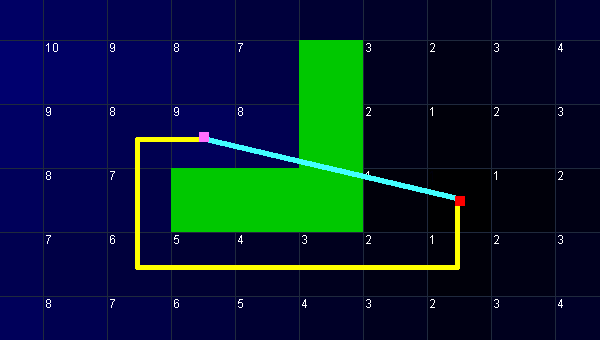
下面,你可以看到路径距离和直线距离的区别。红色是目标点,粉色是随便点的一个起点。渲染为绿色的是不可通行的格子。如你所见,路径距离(黄色)是9,白色直线距离(浅蓝色)大概是4.12。
每个格子左上角的数字显示的是与目标的路径距离,由热力图生成算法计算得出。注意两点之间可能有不止一条路径距离;本文中我们只对最短的感兴趣。

热力图生成算法是一个*wavefront 算法*。从目标处开始取值为0,然后向外流动来填满所有可通行的区域。有两步骤:
– 从目标格开始,标记路径距离为0.
– 然后,每个已标记格子周围找到未标记的相邻格子,把他们标记为`前一个格子的路径距离+1`
– 重复,直到可抵达的全部格子被标记满。
注意:wavefront算法是一个网格上的广度优先搜索,记录了它移动到每个格子全程走了多少步。这有时候也被称为`brushfire算法`。
## 生成矢量场
现在我们已经有生成好的每个格子与目标点的路径距离,我们可以容易确定通往目标的路径。在运行时为每个寻路者逐帧计算也是可行的,但把矢量场一次计算好,然后让所有寻路者引用这个矢量场的做法通常更好。
矢量场在每个格子存储一个矢量,指向通往目标的斜角。这有一幅可视化的矢量场,这些矢量从各格子中心全程指向通向目标(红色)的最短路径。

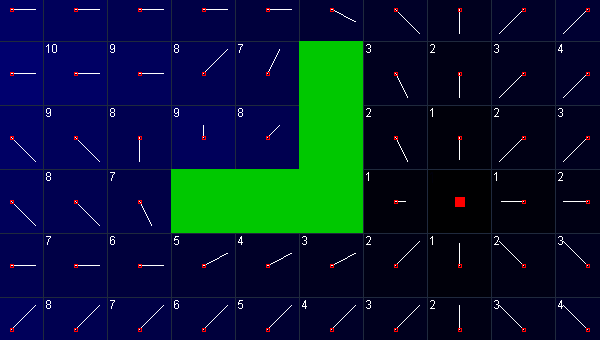
矢量场通过检查热力图每次生成一个格子。x和y是分别计算的:
“`
Vector.x = left_tile.distance – right_tile.distance
Vector.y = up_tile.distance – down_tile.distance
“`
注意:每个格子的`distance`变量存的就是之前wavefront算法计算好的路径距离。
如果引用的格子(上下左右)是无法抵达的,也就没有可用的距离数据,那么直接用当前格子的距离值作为替代。当路径矢量被粗略计算好后,再归一化一下,避免之后数据出现错位问题。
## 寻路者的移动
既然现在矢量场已经被计算好了,寻路者就很容易计算移动量。设`vector_field(x,y)`返回已计算好的`(x,y)`格处的矢量,`desired_velocity`是一个纯量,以下为计算在格子`(x,y)`处的粒子的速度:
“`
velocity_vector = vector_field(x, y) * desired_velocity
“`
粒子只需要开始按照矢量指示的方向移动就行了。这是最简单的方式,而**流场**可用于实现更复杂的移动系统。
比如,这篇文章[Understanding Steering Behaviors](http://gamedev.tutsplus.com/series/understanding-steering-behaviors/) 里阐述的技术可用于寻路移动。在特定情况,上文中我们计算好的`velocity_vector`被用作`desired_velocity`,转向行为会负责在每个时间片计算真正的移动量。
### 局部最优
计算移动的时候,有时会出现一个问题,称作`局部最优`。当格子上同时有2个最优(最短)路径可以抵达目标时出现。
下图中可看到此问题。粉色格子处有一个路径矢量分量x和y皆为0。

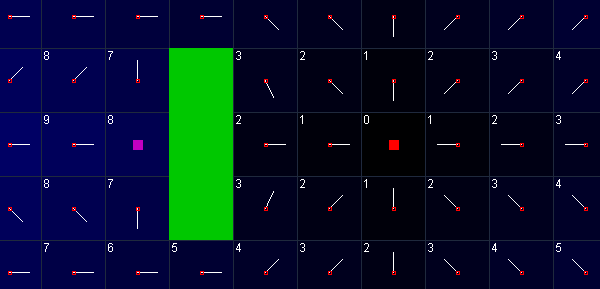
局部最优会导致寻路者卡住,它们引用了一个无法指引前进方向的矢量场。当这种情况发生时,寻路者会持续定在那一格不动,直到修复。
我发现解决这个问题最简明的方法是把热力图和矢量场细分一次。热力图和矢量场的每格被拆分为4小格。细分后的网格,问题依然存在,它只是略微减小了。
真正管用的是用细分后的4个小格用作目标格,而非仅有1个目标格。要做到这样,我们必须修改第一步骤里的生成热力图的算法。我们之前是只放一个目标格子,起始路径距离为0,现在我们放4个靠在一起的格子作目标。
有很多方式来选取这4个格子,但如何选择基本上是无关紧要的——只要这四个格子是临近的、可通行的,这技术就可行。
这有一个改过的步骤,用来做热力图生成:
– 从4个目标格子开始,4个格子全部标记路径距离为0
– 然后,每个已标记格子周围找到未标记的相邻格子,把他们标记为`前一个格子的路径距离+1`
– 重复,直到可抵达的全部格子被标记满。
至此,这是最终结果,可清晰看出,局部最优问题已被终结。


最燃这个解法非常简明,但远不够理想。用这方法意味着计算热力图和矢量场消耗了4倍时间,因为增加到了4倍的网格。
其他解法需要在这问题基础上做一些核查,查明应去的朝向,这个核查会显著降低粒子移动的计算。而我的做法,细分地图可能是最佳选项。
## 总结
希望这个教程教会了你在网格世界中实现基于目标的矢量场寻路。记住,这类型寻路的核心都在于:粒子随着格子的距离函数(前往目标)的斜率移动。
实现略复杂些,但可拆解为下面三个可管理的步骤:
– 热力图生成
– 矢量场生成
– 粒子移动

